Vrtula a jej výkon
Přidané: 19. 4. 2010 o 13:33 | ID článku: CLA42 | Zobrazeno: 24216x | Komentářů: 5 | Autor: arij
Vrtule její výkon.
S masivním vstupem elektropohonu na scénu se objevily problémy, které sice existovaly vždycky, ale nebyly tak důležité jako u elektropohonu: Špatně použitý spalovací motor sice odmítne spolupráci ale nejspíš se nezničí. Špatně sestavený řetězec vrtule-(převodovka)-elektromotor-regulátor-baterie fungovat může. Buďto ovšem s malou účinností, nebo jenom do chvíle, než dojde ke zničení některé části řetězu. Elektromotory mají nejrůznější velikost, jejich hřídele se otáčejí nejrůznějšími otáčkami. Možnost omylu (zejména) použitím nevhodné vrtule nebo jiné nevhodné části pohonného řetězce je obrovská.
Problematika vrtule a elektřiny se často podceňuje, snad proto, že nejsou vidět. Ale krychlička vzduchu o straně 10 metrů má hmotnost 1,2 TUNY (teprve s touto znalostí se hurikány chápou správně). 230 Voltů může zabít, když máte smůlu.
Teorie vrtule je velmi obtížná, zejména proto, že proudění je výrazně trojrozměrné. Začalo se na ní pracovat již před cca 200 lety. Jistě je velmi zajímavé, že vlastní teoretické práce na vrtuli [1] umožnily i epochální úspěch bratří Wrightů před 100 lety. Analytické výpočty vrtule vrcholily cca během 2. světové války. Pro nás relativně snadno dostupná literatura je [2], [3], [4], [5].
V poslední době nastoupily numerické výpočty proudění pomocí výkonných počítačů a dokonalých programů (např. FLUENT), které dokážou namodelovat trojrozměrné vrtule, trojrozměrné proudění, stlačitelnost a vazkost vzduchu. Cena programů a obtížnost jejich obsluhy vyžadují vysoce specializované pracoviště. Výsledná cena výpočtů je patřičně vysoká.
Matematické modelování
Matematické modelování fyzikálních jevů si lidé vymysleli proto, aby se nemuselo pořád všechno zkoušet, ověřovat, platit peníze na neúspěšné pokusy. Pokud se nám podaří matematicky namodelovat to co nás zajímá, budeme si umět rychle a jednoduše spočítat a vysvětlit to, co se vlastně děje. Současně také pochopíme, co máme změnit, proč a jak.
Jak chápat matematické vzorce
Za matematický model lze pokládat každý vzoreček. Vzorec ovšem není shluk písmenek, do kterého se místo písmenek dosadí čísla a ono to vyjde. Správně a na první pokus. V první řadě se musíme dívat na vzorec jako na vysvětlení fyzikálního jevu.
Teprve v druhé řadě je možno vzorec použít pro výpočet. To už často není kupodivu tak důležité nebo to někdo už udělal formou dostupného programu pro počítač. Důležitější je pochopení smyslu vzorce.
Protože je celkem známo, že řadě lidí jsou vzorce proti srsti, přestávají číst a otráveně odvracejí oči, co nejvíce je omezíme a budeme je vyjadřovat i slovně.
1. VRTULE
1.1. Teoretické základy pohonu pomocí vrtule
Pro úplnost by neměly chybět. Klasický matematický model vrtule je postaven na obrázku 1. Jedná se o využití věty o změně hybnosti - např. [5].
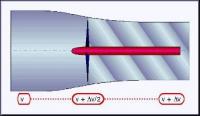
Po aplikaci věty o změně hybnosti zjistíme, že
Tah vrtule T je
T = m x delta v (1)
Tah = průtočné množství tekutiny diskem o průměru vrtule (v kg/sec) x přírůstek rychlosti tekutiny, který vrtule způsobila.
Průtočné množství:
m = průřez (plocha disku vrtule) x hustota vzduchu x rychlost
Přírůstek rychlosti:
delta v = rychlost za vrtulí - rychlost před vrtuli
Výkon je síla (= tah) x rychlost:
P = T x v (2)
Poznámky:
1. Všimněte si, že v tomto fyzikálním modelu se nemusí jednat o vrtuli ale jen o "zařízení, které umí nějakým způsobem urychlit tekutinu". Takže úplně stejný vzorec platí i třeba pro tah proudového motoru, který stojí v obrázku 1 na místě vrtule.
2. V tomto matematickém modelu je úplně lhostejné, jestli vrtule stojí (ventilátor) nebo letí na špičce trupu letadla. Důležitý je jen přírůstek rychlosti. Tekutina se v obou případech relativně k vrtuli pohybuje. V reálu to ovšem přesně totéž není.
1.2. Co je to průměr a stoupání vrtule
Zdánlivě snadné otázka ale kupodivu ne úplně jednoduchá.
K vysvětlení použijeme porovnání vrtule a křídla.
Průměr vrtule je analogický rozpětí křídla. Zhruba řečeno: průměr vrtule odpovídá rozpětí křídla (obr. 2)
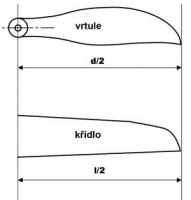
Stoupání vrtule je analogické úhlu náběhu profilu křídla.
Sebedokonalejší profil křídla nedá vhodný vztlak, pokud nebude nastaven pod vhodným úhlem náběhu. Všichni to chápou, nikdo to neudělá špatně, ono to skoro ani nejde moc zkazit. U vrtule se to dá zkazit dost lehce.
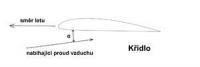
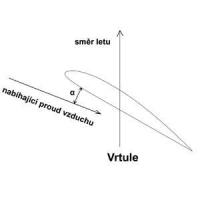
V obrázku 3 je přitom úhel náběhu definován jako úhel mezi směrem nabíhajícího proudu vzduchu a spojnicí náběžné a odtokové hrany profilu (z hlediska proudění je spojnice náběžné a odtokové hrany pouze zcela náhodná přímka, od které se měří úhly).
Sebedokonalejší vrtule nepotáhne, když její list bude mít buď
- příliš malé stoupání (aerodynamická síla bude velmi malá nebo bude dokonce mířit opačným směrem) nebo
- příliš velké stoupání (příliš velký úhel náběhu způsobí odtržené proudění).
To se naopak zkazí velmi snadno, protože do toho není tak vidět. Skutečný úhel náběhu vrtulového listu vůči proudu vzduchu je dán geometrií vrtule, ale také jejími otáčkami a rychlostí letu.
Průměr a stoupání jsou dvě nezávislé veličiny, jedna nemůže žádným bezprostředním způsobem nijak "zastoupit" druhou.
Poznámka:
Občas je možno dočíst se názor, že pro daný motor by měl být součet průměru vrtule a stoupání konstantní. Není tomu tak. Analogicky by se přece sečítalo rozpětí křídla s jeho úhlem náběhu - ale to jistě nikoho nenapadne.
Přesnější definice velikosti natočení listu vrtule
Pro velikost natočení vrtulového listu se nejčastěji používá pojem "stoupání" a dosud jsme se pro jednoduchost od této zvyklosti neodchýlili. Není to ale správné. Stoupání" není totiž možno ztotožnit s úhlem natočení listu.
Důležitým a jednoznačným údajem je opravdu úhel natočení vrtulového listu.
Stoupání je délka, o kterou se vrtule "zavrtá do myšleného tělesa" při jednom otočení.
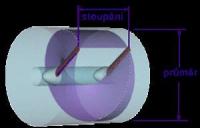
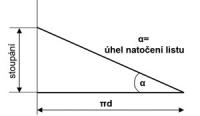
Pokud si rozvineme do roviny povrch válce, po kterém se otáčí špička vrtule, dostaneme na této rovině pravoúhlý trojúhelník, u kterého:
jedna odvěsna má délku obvodu kruhu
druhá odvěsna je stoupání
a pak tedy úhel v trojúhelníku, po jehož přeponě cestuje špička vrtule, je dán oběma odvěsnami, přesně
alfa = arctg (stoupání/obvod) (3)
Podstatný údaj, úhel natočení, je tedy dán POMĚREM stoupání a obvodu.
Příklad:
Stejný úhel natočení jako má vrtule 8x4 má tedy vrtule 16x8 a tyto dvě vrtule jsou si podobné.
Úhel natočení vrtulového listu (alfa) se standardně udává ve vzdálenosti 75% od osy vrtule. Takže z toho vyjde
alfa=180/pi * ARCTG (stoupání/(0,75 * pi* průměr)) . ve stupních (4)
Příklad pro vrtule GWS Slow Fly
Vrtule GWS 8/4,3 12,9
°Vrtule GWS 9/4,7 12,5
°Vrtule GWS 10/4,7 11,3
°Vrtule GWS 11/4,7 10,3
°Příklad pro modré vrtule Icarus Shock Flyer:
Vrtule 9 x 5 má úhel 13,5
°Vrtule 10,5 x 5 má úhel 11,5
°Stejné stoupání neznamená stejný úhel, důležitý rozměr je úhel.
Podobně jako u křídla, změna úhlu o jediný stupeň znamená hodně.
Poznámka:
Častý dotaz: Koupil jsem si listy pro sklopku třeba 9x5. Počítá se do průměru délka trámku?
Odpověď: Listy jsou navrženy pro průměr (přes všechno) 9 palců. Pokud použijete trámek, se kterým je celkový průměr jiný, vrtuli jste asi trochu pokazili a určitě trochu změnili její průměr a vlastně i natočení listu: list je oproti předpokladu výrobce na radiální linii posunutý. Tím se na 75% průměru dostal jiný úhel natočení, než ten, který tam chtěl mít výrobce.
Průměr vrtule se samozřejmě počítá "přes všechno". V základním vzorci (1) pro tah resp. výkon je důležité množství vzduchu, které prochází celým diskem vrtule.
Poznámka:
Výrobci udávané stoupání v názvu vrtule se často liší od skutečné hodnoty stoupání vrtule. Například vrtule Aeronaut CAM Carbon 30x20cm má skutečné stoupání 22cm.
1.3. Další vlastnosti vrtule
Dosud jsme se tvarem vrtule nezabývali. Nakonec - návrháři to udělali za nás.
Vrtule je ale vlastně rotující křídlo o velmi nízké štíhlosti, takže proudění je výrazně trojrozměrné: vzduch proudí také směrem od kořene ke špičce.
Aby stoupání bylo konstantní, vrtule musí být zkroucená. Vzhledem k nízké štíhlosti listu nemusí být přesná šroubovice ideální tvar. Na šroubovici může být "naroubováno" další zkroucení, podobně jako má křídlo "negativy" - "winglety" - atd.
1.4. Počet listů
Má samozřejmě výrazný vliv, dá se vyčíslit [6]:
Dvoulistá vrtule o průměru D je ekvivalentní s třílistou vrtulí o průměru 0,92D (jiná literatura udává 0,9D).
Dvoulistá vrtule o průměru D je ekvivalentní se čtyřlistou vrtulí o průměru 0,87D (jinde 0,84D).
1.5. Podobnost vrtulí
Pokud srovnáváme vrtule, musíme si uvědomit, zda se jedná o tvarově podobné vrtule jedné "rodiny" nebo o úplně rozdílné tvary a podle toho uvažovat. Pokud budeme srovnávat vrtule jedné rodiny, dá se očekávat, co se stane třeba při zvětšení průměru. Vrtule různých rodin se tak jednoduše porovnávat nedají.
Do tvaru vrtule patří také její profil, šířka listu atd.
Pozn.: Vrtule Icarus 9x5 s prohnutým profilem odebírá větší výkon, než vrtule GWS 9x5 s profilem s rovnou spodní stranou.
Širší vrtule odebírá také obvykle větší výkon.
1.6 Účinnost vrtule
Volba nejvhodnější vrtule může být hezký oříšek, protože některé požadavky si odporují a optimalizace je obtížná.
Poměrně rozšířeným názorem je, že malá vrtule má nízkou účinnost a velká vrtule účinnost větší. Zdůvodňuje se to tak, že větší profil větší vrtule má větší Reynoldsovo číslo. Bohužel se jedná o pověru. Není to tak jednoduché.
Převodovka umožní použít větší vrtuli, ta se otáčí menšími otáčkami. Reynoldsovo číslo, které je úměrné součinu rychlosti a tětivy (hloubka profilu)je pro oba případy zhruba shodné.
Skutečnou příčinu lepší účinnosti větší vrtule musíme hledat jinde: Účinnost je závislá na úhlu natočení listu. Nejlepší hodnoty dosahuje, pokud je úhel natočení listu v 75% délky listu cca 20 stupňů. To odpovídá zhruba "čtvercové" vrtuli (průměr = stoupání).
Vyplývá to z principu funkce vrtule (vrtule s velkým úhlem natočení listu využije více energie na užitečné urychlení (rozdíl rychlostí, viz vzorec (1)), vrtule s malým stoupáním maří více energie pro rotaci proudu za vrtulí).
Velká vrtule (u modelu s převodovkou) se točí pomaleji, z toho plyne, že je možné použít listy s větším natočením a tedy s větší účinností. Taková vrtule bude lépe fungovat při letu "cestovní, návrhovou" rychlostí. Při letu malou rychlostí ale dobře pracovat nebude, protože proudění se od silně zkrouceného listu odtrhává. Zrychlování při startu nebo z nízké rychlosti bude pomalé.
Závěry:
1. Vrtule s malým stoupáním lépe zrychluje, nejvyšší rychlost není vysoká.
2. Vrtule s velkým stoupáním poskytne vysokou rychlost a velkou účinnost, zrychlení modelu je pomalejší (to vysvětluje třeba nemotorné starty modelů F3D, které pak letí neuvěřitelně vysokou "cestovní" rychlostí).
Elektromotory poskytují obrovský rozsah otáček a spolu s případným využitím převodovky je tento rozsah ještě větší.
S problémem si můžete pohrát u počítače pomocí jednoduchého prográmku (např. [7]) který opravdu funguje. Z tabulky v programu je závislost účinnosti na velikosti úhlu nakroucení bezprostředně viditelná.
Poslední slovo má ovšem pokus v letu, vaše požadavky i zvyklosti.
2. VÝKON
2.1. Výkon vrtule
Vzorec jsme již definovali (2) ale ve formě, která není v praxi příliš použitelná. Rychlost tekutiny se měří špatně. Proto se přechází k následující formě, kde je rychlost tekutiny jistým způsobem vyloučena. Podle tohoto vzorce nebudeme nic počítat, je ale nesmírně důležitý pro pochopení vlivu parametrů.
Výkon vrtule = Cp x ro x otáčky** 3 x průměr** 5 (5)
Výkon výkon (W)
Cp konstanta
ro hustota vzduchu (kg/m3)
ot otáčky (1/s)
průměr (m)
Poznámka: jsou definovány základní jednotky, v praxi to může být jinak a do Cp mohou být zahrnuty přepočtové konstanty jednotek. Konstanta Cp je dána pro tzv. rodinu tvarově podobných vrtulí.
2.2. Závěry, plynoucí ze vzorce pro výkon.
Z vzorce (5) vyplývá, že:
1. Výkon je úměrný třetí mocnině otáček. Jinými slovy: Pokud chcete zvýšit otáčky stejné vrtule o 10%, musíte zvýšit výkon o 33% (1,13/13=1,33).
2. Výkon je úměrný páté mocnině průměru. Pokud zvětšíte průměr vrtule o 10%, musíte (pro zachování otáček !!!) zvýšit příkon o 60% !!! Výkon je výrazně závislý na průměru vrtule. Malé zvětšení průměru vrtule může snadno vést k nepředvídatelným následkům: spálení motoru, regulátoru, předčasné opotřebení baterie. Pokud baterie není dostatečně tvrdá (rychle klesá napětí), vede často velká vrtule k nevysvětlitelnému odpojování motoru od regulátoru.
Poznámka: Zdá se, že lidský "selský rozum" je schopen dobře chápat jen přímou úměru, tj. "malá změna příčiny" vede k "malému důsledku". V přírodě tak ale všechno nefunguje.
- Kinetická energie je úměrná druhé mocnině rychlosti. Auto, jedoucí rychlostí 70 km/hod má dvojnásobnou kinetickou (někdy tedy destrukční) energii, než auto, jedoucí rychlostí 50 km/hod (4900/2500 = cca 2)
- Pokud zvýšíte počet článků baterie ze 7 na 8, nezvýšili jste výkon o 14% (8/7 = 1,14) ale o 31% až 49% protože výkon je úměrný třetí mocnině otáček, které rostou s napětím téměř lineárně.
Pokud náš rozum špatně chápe již 2. mocninu, pak 5. mocnina je zcela mimo možnosti lidského odhadu a nezbývá, než počítat a/nebo měřit.
2.3. Jak dimenzovat motor, regulátor, baterie.
Úvahy budeme dělat pro jeden libovolně zvolený motor, protože pro následující úvahy musíme mít nějaký pevný bod.
Z předchozího textu plyne, že odebíraný výkon závisí jenom na vrtuli.
Výkon je dán jako součin napětí a proudu. V prvním kroku budeme uvažovat konstantní napětí. Se zvětšováním průměru vrtule tedy poroste odebíraný výkon a protože napětí se nemění, poroste proud. Podle takto zjištěného proudu je nutné dimenzovat motor, regulátor, baterie.
Pokud výkon nestačí, můžete zvýšit počet článků (= napětí). Současně s tím je ovšem třeba si uvědomit, že zvýšením napětí se zvýšil i proud. Kontrolujte, zda proud nepřesáhne bezpečné hranice částí pohonného řetězu .
Vždy kontrolujte, zda naměřený proud odpovídá alespoň zhruba proudu pro maximální účinnost motoru. Pokud motor přetěžujete, snižuje se jeho účinnost. Elektrická energie se pak používá na pouhé ohřátí motoru, ne na otáčení vrtule.
2.4 Statické měření výkonu vrtule
Statický výkon reálné vrtule se dá relativně snadno změřit pomocí dynamometru. Vrtule je normálně upevněna na hřídeli elektromotoru. Stator (nepohyblivá část) elektromotoru je uložen ve dvojici kuličkových ložisek, tak, aby se mohl volně pootáčet. Pomocí páky a váhy se měří moment, kterým je elektromotor otáčen proti rotaci vrtule (pozor, neplést si s pojmem statický tah, který pro hodnocení vrtule je prakticky bezcenný). Výkon vrtule se dá vyjádřit velmi jednoduše
Výkon vrtule = moment x otáčky (6)
2.5 Statické versus letové poměry
Jak už bylo uvedeno, výchozí matematický model je založen na předpokladu relativní rychlosti mezi tekutinou a vrtulí a nezáleží na tom jestli se vrtule točí na stole nebo letí na letadle. To ovšem není v reálném světě pravda.
Statické měření je možno provést doma na stole. Je to jednoduché a pohodlné. Pokud se nechceme zabývat komplikovaným měřením proudu za letu nebo složitými výpočty, vlastně ani nic jiného nezbývá. Výsledky měření jsou zajímavé a důležité. Nechceme přece zničit motor už před startem.
Problém je ovšem s přenesením statického měření do letu. Mezi modeláři se traduje, že motor se za letu dost významně "odlehčí". Bohužel, tak snadné to není. Špatná zpráva je, že obecné závěry nelze dělat. Dobrá zpráva je, že si tuto skutečnost uvědomujeme a umíme s ní do jisté míry počítat.
Zhruba je možno říci následující:
Pokud použijeme vrtuli s malým úhlem natočení (poměr průměru a stoupání cca 2:1), motor se s velkou pravděpodobností za letu opravdu odlehčí. Může to být ale jen velmi málo a je lepší na to nespoléhat. Diagram zatížení v závislosti na rychlosti může mít dokonce "hrb" [4].
Pokud použijeme vrtuli s velkým úhlem natočení (zhruba "čtvercovou", poměr průměru a stoupání cca 1:1), veškeré odhady jsou z říše snů. Silně natočená vrtule je při statických testech pravděpodobně obtékána s výrazným odtržením proudu, za letu při návrhové rychlosti jsou poměry zcela jiné. Je dost pravděpodobné, že požadovaný výkon za letu dokonce naroste.
Statické měření není sice zdaleka dokonalé ale poskytuje jisté možnosti při porovnávání různých vrtulí, motorů, akumulátorů. Přinejmenším už není třeba střílet úplně naslepo ale je možno si pohony a jejich části snadno a rychle otestovat doma na stole, podle naměřeného proudu dimenzovat a teprve poté ověřit v provozu.
Poznámka:
V předchozím odstavci jsme pochopitelně předpokládali pouze měření a let na plný plyn.
Poznámka:
Statický tah vrtule závisí pouze na typu vrtule a na jejích otáčkách. Díky neznalosti této skutečnosti se zbytečně postavilo mnoho tahoměrů a zbytečně investovalo mnoho času při znovuobjevování dávno objeveného. Pro zjištění statického tahu stačí odměřit otáčky, zjistit si dva koeficienty a tah jednoduše vypočítat. Všechny běžné vrtule jsou dávno odměřené. Kdyby se vám nechtělo počítat (asi ne, proto ani vzoreček neuvádíme) stačí si otevřít např.
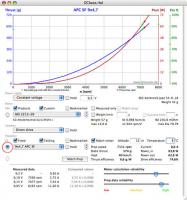
www.elektromodellflug.de (www spravuje německý elektro-guru G. Giesse), nainstalovat program DRIVE CALCULETOR a najít diagram pro danou vrtuli.
Jeden je pro ilustraci na obrázku. Stačí odměřit otáčky a odečíst statický tah (modrá křivka). Pomocí červené křivky lze pro dané otáčky odečíst výkon vrtule.
Program nabízí ovšem daleko větší možnosti.
3. VÝPOČTY
Pokud byste si rádi něco spočítali, je to docela snadno možné. Výchozí vzorec pro výkon (5) je možno pro danou vrtuli zjednodušit (Cp, ro, průměr považujeme za konstanty) na:
výkon = konstanta1 x otáčky ** konstanta 2 (7)
(konstanta2 = cca 3)
Obě konstanty je možno zjistit poměrně snadno sadou měření na dynamometru a jejich vyhodnocením. Nemusíte to ale dělat, konstanty pro velké množství běžných vrtulí již zpracovalo velké množství autorů. Tabulky jsou dostupné (a přeložené) např. na našich webových stránkách [6], [7]. Pro usnadnění výpočtu je možno (ale není nutno) použít Emeter a/nebo související programy které jsou volně dostupné.
Je ovšem nutno si uvědomit, že měření byla statická a výsledky pro letové poměry jsou pouze orientační.
Podobným způsobem, jen s jinými konstantami, je možno získat pro danou vrtuli i vztah mezi otáčkami a tahem. Pro dost přesné zjištění velikosti statického tahu stačí tedy naměřit otáčky a přepočíst tah. Konstanty pro některé vrtule jsou opět uvedené v programu pro Emeter (ale Emeter opět nepotřebujete).
4. MĚŘENÍ
Pomocí dostupné techniky (Eagletree Elogger, Emeter, přístroj CM50, výškoměr ALTI) byla provedena některá statická a letová měření. Měření trvají nějaký čas, při létání nesmí foukat atd, a není jich tedy mnoho. Nicméně poskytují alespoň částečný obrázek o vlastnostech pohonů, o kterých jsme dosud věděli hodně málo a tušili špatně.
K prvnímu měření
byl použit model Super Zoom od firmy Hacker, elektromotor AC MINI XT, baterie Lipol Dualsky Xpower 750-3s, regulátor Castle Creations Phoenix 25 v základním nastavení, vrtule GWS 9x5 HD.
Rychlost letu byla měřena za bezvětří na bázi 100 metrů, několikanásobným průletem.
Všechna data byla získána průměrováním několika měření. Nikdy nedošlo k výrazné odchylce. Proud byl měřen přístrojem CM50 v okamžicích podle povelů, přenášených RC systémem.

Statické měření:
10,2 V - 11,4 A - 8565 ot/min
Letové měření:
Vodorovný let na plný plyn: rychlost 56 km/hod, 8,8 A
Došlo tedy k poklesu proudu o 23%.
Poznámka: Zvolená baterie nebyla vhodná (malá kapacita), což se potvrdilo jejím krátkým životem.
Další měření bylo provedeno s elektrovětroněm Q10 o rozpětí cca 1800 mm a hmotnosti cca 500 gramů. Motor AC MINI T (převinutý na 6 závitů), baterie Xpower 1700-2s, sklopná vrtule Aeronaut 9x5.

Statické měření:
7,14V - 23,6 A - 8730 ot/min
Letové měření při stoupání v poměru cca 6 metrů/sec (tj. cca 180 metrů výšky za 30 sekund).
Provedeno 5 měření během 30 sekundového stoupání, průměrný odběr byl 20,5 A (pokles proudu byl velmi pozvolný). Motor je sice přetěžován ale v režimu časově krátkého zatížení bez regulace mu to zjevně nevadí. Pokles proudu byl pouhých 13 %, menší než jsme očekávali.
Závěry z našich měření:
1. Největší odběr proudu byl při statickém měření.
2. Pokles zatížení za letu nebyl ve srovnání se statickými zkouškami tak dramatický jak se očekávalo. Došlo k poklesu proudu o cca 10-20%.
3. Výsledků bylo dosaženo s vrtulemi o poměru průměru a stoupání zhruba 2:1.
Výsledky našich měření rozhodně nelze zobecňovat, zejména nemusí fungovat pokles proudu za letu. Mohou sloužit jen jako jisté vodítko k Vašim pokusům.
Poznámky k měření:
Statické měření je možno provádět v nejhorším případě s levným digitálním ampérmetrem. Lepší je pro tento účel analogový přístroj. Klešťové ampérmetry pro měření stejnosměrného proudu jsou dost drahé a pouze jednoúčelové. Rozhodně tedy stojí za úvahu použít přístroje, které jsou pro tato měření specializovány a často jsou víceúčelové. Dále existují přístroje, které měří v okamžiku podle povelu vysílače nebo přístroje, které shromažďují data během letu. Data se pak vyhodnocují na počítači a dají se libovolně zpracovat.
Přístroje, které naměří pouze maximální hodnoty během letu, jsou dobré jen pro velmi hrubou orientaci: naměří maximální proud - ale pravděpodobně při plném plynu těsně před startem, naměří maximální otáčky motoru - ale při jeho náhodném odlehčení. Pro vážnější práci se opravdu nehodí.
5. ZÁVĚR
Pokud jste čekali jednoznačný návod na řešení vrtule a souvisejícího pohonného řetězce a nedostali ho, nezlobte se. Ono to tak snadné není. Tím není jistě řečeno že optimální vrtule se nedá vypočíst. To je vyhrazeno několika specialistům a je zcela mimo možnosti běžného modeláře.
Optimalizace vrtule pro model F3D, letící konstantní "cestovní" rychlostí 350 km/hod, je ovšem úplně jiná úloha, než vybrat vhodnou vrtuli pro sportovní éro pro zábavu, které má létat v širokém rozsahu rychlostí. Předpokládáme, že naši čtenáři stojí spíše na té druhé straně. Specialisté pylonáři naši pomoc určitě nepotřebují.
Pokud jsme pomohli k alespoň částečnému vylepšení Vaší orientace v problematice, splnil článek účel a my děkujeme za trpělivost.
6. PODĚKOVÁNÍ
Děkuji RNDr Z. Hubáčkovi za významnou pomoc při psaní článku.
Ing. L. Bendovi děkuji za cenné kritické připomínky.
Literatura:
[1] Ash, Miley, Landman, Hyde: Evolution of Wright Flyer Propellers betweem 1903-1912 AIAA Journal 2001-0309
[2] Hořejší Milan: Profil, křídlo, vrtule
[3] Benda Lubomír: Vrtule - Seriál v časopise Modelář 1985
[4] Benda Lubomír: RCR 10/2005
[5] Hepperle Martin: Propulsion by propellers http://www.mh-aerotools.de
[6] Connolly: Prop talk http://www.hyperion.hk
[7] Hořejší Ivan: www.horejsi.cz
[8] Hubáček Zdeněk: Osobní sdělení
Článok prevzatý zo stránky : http://www.horejsi.cz/Pages/ListClanky.aspx
S masivním vstupem elektropohonu na scénu se objevily problémy, které sice existovaly vždycky, ale nebyly tak důležité jako u elektropohonu: Špatně použitý spalovací motor sice odmítne spolupráci ale nejspíš se nezničí. Špatně sestavený řetězec vrtule-(převodovka)-elektromotor-regulátor-baterie fungovat může. Buďto ovšem s malou účinností, nebo jenom do chvíle, než dojde ke zničení některé části řetězu. Elektromotory mají nejrůznější velikost, jejich hřídele se otáčejí nejrůznějšími otáčkami. Možnost omylu (zejména) použitím nevhodné vrtule nebo jiné nevhodné části pohonného řetězce je obrovská.
Problematika vrtule a elektřiny se často podceňuje, snad proto, že nejsou vidět. Ale krychlička vzduchu o straně 10 metrů má hmotnost 1,2 TUNY (teprve s touto znalostí se hurikány chápou správně). 230 Voltů může zabít, když máte smůlu.
Teorie vrtule je velmi obtížná, zejména proto, že proudění je výrazně trojrozměrné. Začalo se na ní pracovat již před cca 200 lety. Jistě je velmi zajímavé, že vlastní teoretické práce na vrtuli [1] umožnily i epochální úspěch bratří Wrightů před 100 lety. Analytické výpočty vrtule vrcholily cca během 2. světové války. Pro nás relativně snadno dostupná literatura je [2], [3], [4], [5].
V poslední době nastoupily numerické výpočty proudění pomocí výkonných počítačů a dokonalých programů (např. FLUENT), které dokážou namodelovat trojrozměrné vrtule, trojrozměrné proudění, stlačitelnost a vazkost vzduchu. Cena programů a obtížnost jejich obsluhy vyžadují vysoce specializované pracoviště. Výsledná cena výpočtů je patřičně vysoká.
Matematické modelování
Matematické modelování fyzikálních jevů si lidé vymysleli proto, aby se nemuselo pořád všechno zkoušet, ověřovat, platit peníze na neúspěšné pokusy. Pokud se nám podaří matematicky namodelovat to co nás zajímá, budeme si umět rychle a jednoduše spočítat a vysvětlit to, co se vlastně děje. Současně také pochopíme, co máme změnit, proč a jak.
Jak chápat matematické vzorce
Za matematický model lze pokládat každý vzoreček. Vzorec ovšem není shluk písmenek, do kterého se místo písmenek dosadí čísla a ono to vyjde. Správně a na první pokus. V první řadě se musíme dívat na vzorec jako na vysvětlení fyzikálního jevu.
Teprve v druhé řadě je možno vzorec použít pro výpočet. To už často není kupodivu tak důležité nebo to někdo už udělal formou dostupného programu pro počítač. Důležitější je pochopení smyslu vzorce.
Protože je celkem známo, že řadě lidí jsou vzorce proti srsti, přestávají číst a otráveně odvracejí oči, co nejvíce je omezíme a budeme je vyjadřovat i slovně.
1. VRTULE
1.1. Teoretické základy pohonu pomocí vrtule
Pro úplnost by neměly chybět. Klasický matematický model vrtule je postaven na obrázku 1. Jedná se o využití věty o změně hybnosti - např. [5].

Po aplikaci věty o změně hybnosti zjistíme, že
Tah vrtule T je
T = m x delta v (1)
Tah = průtočné množství tekutiny diskem o průměru vrtule (v kg/sec) x přírůstek rychlosti tekutiny, který vrtule způsobila.
Průtočné množství:
m = průřez (plocha disku vrtule) x hustota vzduchu x rychlost
Přírůstek rychlosti:
delta v = rychlost za vrtulí - rychlost před vrtuli
Výkon je síla (= tah) x rychlost:
P = T x v (2)
Poznámky:
1. Všimněte si, že v tomto fyzikálním modelu se nemusí jednat o vrtuli ale jen o "zařízení, které umí nějakým způsobem urychlit tekutinu". Takže úplně stejný vzorec platí i třeba pro tah proudového motoru, který stojí v obrázku 1 na místě vrtule.
2. V tomto matematickém modelu je úplně lhostejné, jestli vrtule stojí (ventilátor) nebo letí na špičce trupu letadla. Důležitý je jen přírůstek rychlosti. Tekutina se v obou případech relativně k vrtuli pohybuje. V reálu to ovšem přesně totéž není.
1.2. Co je to průměr a stoupání vrtule
Zdánlivě snadné otázka ale kupodivu ne úplně jednoduchá.
K vysvětlení použijeme porovnání vrtule a křídla.
Průměr vrtule je analogický rozpětí křídla. Zhruba řečeno: průměr vrtule odpovídá rozpětí křídla (obr. 2)

Stoupání vrtule je analogické úhlu náběhu profilu křídla.
Sebedokonalejší profil křídla nedá vhodný vztlak, pokud nebude nastaven pod vhodným úhlem náběhu. Všichni to chápou, nikdo to neudělá špatně, ono to skoro ani nejde moc zkazit. U vrtule se to dá zkazit dost lehce.


V obrázku 3 je přitom úhel náběhu definován jako úhel mezi směrem nabíhajícího proudu vzduchu a spojnicí náběžné a odtokové hrany profilu (z hlediska proudění je spojnice náběžné a odtokové hrany pouze zcela náhodná přímka, od které se měří úhly).
Sebedokonalejší vrtule nepotáhne, když její list bude mít buď
- příliš malé stoupání (aerodynamická síla bude velmi malá nebo bude dokonce mířit opačným směrem) nebo
- příliš velké stoupání (příliš velký úhel náběhu způsobí odtržené proudění).
To se naopak zkazí velmi snadno, protože do toho není tak vidět. Skutečný úhel náběhu vrtulového listu vůči proudu vzduchu je dán geometrií vrtule, ale také jejími otáčkami a rychlostí letu.
Průměr a stoupání jsou dvě nezávislé veličiny, jedna nemůže žádným bezprostředním způsobem nijak "zastoupit" druhou.
Poznámka:
Občas je možno dočíst se názor, že pro daný motor by měl být součet průměru vrtule a stoupání konstantní. Není tomu tak. Analogicky by se přece sečítalo rozpětí křídla s jeho úhlem náběhu - ale to jistě nikoho nenapadne.
Přesnější definice velikosti natočení listu vrtule
Pro velikost natočení vrtulového listu se nejčastěji používá pojem "stoupání" a dosud jsme se pro jednoduchost od této zvyklosti neodchýlili. Není to ale správné. Stoupání" není totiž možno ztotožnit s úhlem natočení listu.
Důležitým a jednoznačným údajem je opravdu úhel natočení vrtulového listu.
Stoupání je délka, o kterou se vrtule "zavrtá do myšleného tělesa" při jednom otočení.

Pokud si rozvineme do roviny povrch válce, po kterém se otáčí špička vrtule, dostaneme na této rovině pravoúhlý trojúhelník, u kterého:
jedna odvěsna má délku obvodu kruhu
druhá odvěsna je stoupání
a pak tedy úhel v trojúhelníku, po jehož přeponě cestuje špička vrtule, je dán oběma odvěsnami, přesně
alfa = arctg (stoupání/obvod) (3)
Podstatný údaj, úhel natočení, je tedy dán POMĚREM stoupání a obvodu.

Příklad:
Stejný úhel natočení jako má vrtule 8x4 má tedy vrtule 16x8 a tyto dvě vrtule jsou si podobné.
Úhel natočení vrtulového listu (alfa) se standardně udává ve vzdálenosti 75% od osy vrtule. Takže z toho vyjde
alfa=180/pi * ARCTG (stoupání/(0,75 * pi* průměr)) . ve stupních (4)
Příklad pro vrtule GWS Slow Fly
Vrtule GWS 8/4,3 12,9
°Vrtule GWS 9/4,7 12,5
°Vrtule GWS 10/4,7 11,3
°Vrtule GWS 11/4,7 10,3
°Příklad pro modré vrtule Icarus Shock Flyer:
Vrtule 9 x 5 má úhel 13,5
°Vrtule 10,5 x 5 má úhel 11,5
°Stejné stoupání neznamená stejný úhel, důležitý rozměr je úhel.
Podobně jako u křídla, změna úhlu o jediný stupeň znamená hodně.
Poznámka:
Častý dotaz: Koupil jsem si listy pro sklopku třeba 9x5. Počítá se do průměru délka trámku?
Odpověď: Listy jsou navrženy pro průměr (přes všechno) 9 palců. Pokud použijete trámek, se kterým je celkový průměr jiný, vrtuli jste asi trochu pokazili a určitě trochu změnili její průměr a vlastně i natočení listu: list je oproti předpokladu výrobce na radiální linii posunutý. Tím se na 75% průměru dostal jiný úhel natočení, než ten, který tam chtěl mít výrobce.
Průměr vrtule se samozřejmě počítá "přes všechno". V základním vzorci (1) pro tah resp. výkon je důležité množství vzduchu, které prochází celým diskem vrtule.
Poznámka:
Výrobci udávané stoupání v názvu vrtule se často liší od skutečné hodnoty stoupání vrtule. Například vrtule Aeronaut CAM Carbon 30x20cm má skutečné stoupání 22cm.
1.3. Další vlastnosti vrtule
Dosud jsme se tvarem vrtule nezabývali. Nakonec - návrháři to udělali za nás.
Vrtule je ale vlastně rotující křídlo o velmi nízké štíhlosti, takže proudění je výrazně trojrozměrné: vzduch proudí také směrem od kořene ke špičce.
Aby stoupání bylo konstantní, vrtule musí být zkroucená. Vzhledem k nízké štíhlosti listu nemusí být přesná šroubovice ideální tvar. Na šroubovici může být "naroubováno" další zkroucení, podobně jako má křídlo "negativy" - "winglety" - atd.
1.4. Počet listů
Má samozřejmě výrazný vliv, dá se vyčíslit [6]:
Dvoulistá vrtule o průměru D je ekvivalentní s třílistou vrtulí o průměru 0,92D (jiná literatura udává 0,9D).
Dvoulistá vrtule o průměru D je ekvivalentní se čtyřlistou vrtulí o průměru 0,87D (jinde 0,84D).
1.5. Podobnost vrtulí
Pokud srovnáváme vrtule, musíme si uvědomit, zda se jedná o tvarově podobné vrtule jedné "rodiny" nebo o úplně rozdílné tvary a podle toho uvažovat. Pokud budeme srovnávat vrtule jedné rodiny, dá se očekávat, co se stane třeba při zvětšení průměru. Vrtule různých rodin se tak jednoduše porovnávat nedají.
Do tvaru vrtule patří také její profil, šířka listu atd.
Pozn.: Vrtule Icarus 9x5 s prohnutým profilem odebírá větší výkon, než vrtule GWS 9x5 s profilem s rovnou spodní stranou.
Širší vrtule odebírá také obvykle větší výkon.
1.6 Účinnost vrtule
Volba nejvhodnější vrtule může být hezký oříšek, protože některé požadavky si odporují a optimalizace je obtížná.
Poměrně rozšířeným názorem je, že malá vrtule má nízkou účinnost a velká vrtule účinnost větší. Zdůvodňuje se to tak, že větší profil větší vrtule má větší Reynoldsovo číslo. Bohužel se jedná o pověru. Není to tak jednoduché.
Převodovka umožní použít větší vrtuli, ta se otáčí menšími otáčkami. Reynoldsovo číslo, které je úměrné součinu rychlosti a tětivy (hloubka profilu)je pro oba případy zhruba shodné.
Skutečnou příčinu lepší účinnosti větší vrtule musíme hledat jinde: Účinnost je závislá na úhlu natočení listu. Nejlepší hodnoty dosahuje, pokud je úhel natočení listu v 75% délky listu cca 20 stupňů. To odpovídá zhruba "čtvercové" vrtuli (průměr = stoupání).
Vyplývá to z principu funkce vrtule (vrtule s velkým úhlem natočení listu využije více energie na užitečné urychlení (rozdíl rychlostí, viz vzorec (1)), vrtule s malým stoupáním maří více energie pro rotaci proudu za vrtulí).
Velká vrtule (u modelu s převodovkou) se točí pomaleji, z toho plyne, že je možné použít listy s větším natočením a tedy s větší účinností. Taková vrtule bude lépe fungovat při letu "cestovní, návrhovou" rychlostí. Při letu malou rychlostí ale dobře pracovat nebude, protože proudění se od silně zkrouceného listu odtrhává. Zrychlování při startu nebo z nízké rychlosti bude pomalé.
Závěry:
1. Vrtule s malým stoupáním lépe zrychluje, nejvyšší rychlost není vysoká.
2. Vrtule s velkým stoupáním poskytne vysokou rychlost a velkou účinnost, zrychlení modelu je pomalejší (to vysvětluje třeba nemotorné starty modelů F3D, které pak letí neuvěřitelně vysokou "cestovní" rychlostí).
Elektromotory poskytují obrovský rozsah otáček a spolu s případným využitím převodovky je tento rozsah ještě větší.
S problémem si můžete pohrát u počítače pomocí jednoduchého prográmku (např. [7]) který opravdu funguje. Z tabulky v programu je závislost účinnosti na velikosti úhlu nakroucení bezprostředně viditelná.
Poslední slovo má ovšem pokus v letu, vaše požadavky i zvyklosti.
2. VÝKON
2.1. Výkon vrtule
Vzorec jsme již definovali (2) ale ve formě, která není v praxi příliš použitelná. Rychlost tekutiny se měří špatně. Proto se přechází k následující formě, kde je rychlost tekutiny jistým způsobem vyloučena. Podle tohoto vzorce nebudeme nic počítat, je ale nesmírně důležitý pro pochopení vlivu parametrů.
Výkon vrtule = Cp x ro x otáčky** 3 x průměr** 5 (5)
Výkon výkon (W)
Cp konstanta
ro hustota vzduchu (kg/m3)
ot otáčky (1/s)
průměr (m)
Poznámka: jsou definovány základní jednotky, v praxi to může být jinak a do Cp mohou být zahrnuty přepočtové konstanty jednotek. Konstanta Cp je dána pro tzv. rodinu tvarově podobných vrtulí.
2.2. Závěry, plynoucí ze vzorce pro výkon.
Z vzorce (5) vyplývá, že:
1. Výkon je úměrný třetí mocnině otáček. Jinými slovy: Pokud chcete zvýšit otáčky stejné vrtule o 10%, musíte zvýšit výkon o 33% (1,13/13=1,33).
2. Výkon je úměrný páté mocnině průměru. Pokud zvětšíte průměr vrtule o 10%, musíte (pro zachování otáček !!!) zvýšit příkon o 60% !!! Výkon je výrazně závislý na průměru vrtule. Malé zvětšení průměru vrtule může snadno vést k nepředvídatelným následkům: spálení motoru, regulátoru, předčasné opotřebení baterie. Pokud baterie není dostatečně tvrdá (rychle klesá napětí), vede často velká vrtule k nevysvětlitelnému odpojování motoru od regulátoru.
Poznámka: Zdá se, že lidský "selský rozum" je schopen dobře chápat jen přímou úměru, tj. "malá změna příčiny" vede k "malému důsledku". V přírodě tak ale všechno nefunguje.
- Kinetická energie je úměrná druhé mocnině rychlosti. Auto, jedoucí rychlostí 70 km/hod má dvojnásobnou kinetickou (někdy tedy destrukční) energii, než auto, jedoucí rychlostí 50 km/hod (4900/2500 = cca 2)
- Pokud zvýšíte počet článků baterie ze 7 na 8, nezvýšili jste výkon o 14% (8/7 = 1,14) ale o 31% až 49% protože výkon je úměrný třetí mocnině otáček, které rostou s napětím téměř lineárně.
Pokud náš rozum špatně chápe již 2. mocninu, pak 5. mocnina je zcela mimo možnosti lidského odhadu a nezbývá, než počítat a/nebo měřit.
2.3. Jak dimenzovat motor, regulátor, baterie.
Úvahy budeme dělat pro jeden libovolně zvolený motor, protože pro následující úvahy musíme mít nějaký pevný bod.
Z předchozího textu plyne, že odebíraný výkon závisí jenom na vrtuli.
Výkon je dán jako součin napětí a proudu. V prvním kroku budeme uvažovat konstantní napětí. Se zvětšováním průměru vrtule tedy poroste odebíraný výkon a protože napětí se nemění, poroste proud. Podle takto zjištěného proudu je nutné dimenzovat motor, regulátor, baterie.
Pokud výkon nestačí, můžete zvýšit počet článků (= napětí). Současně s tím je ovšem třeba si uvědomit, že zvýšením napětí se zvýšil i proud. Kontrolujte, zda proud nepřesáhne bezpečné hranice částí pohonného řetězu .
Vždy kontrolujte, zda naměřený proud odpovídá alespoň zhruba proudu pro maximální účinnost motoru. Pokud motor přetěžujete, snižuje se jeho účinnost. Elektrická energie se pak používá na pouhé ohřátí motoru, ne na otáčení vrtule.
2.4 Statické měření výkonu vrtule
Statický výkon reálné vrtule se dá relativně snadno změřit pomocí dynamometru. Vrtule je normálně upevněna na hřídeli elektromotoru. Stator (nepohyblivá část) elektromotoru je uložen ve dvojici kuličkových ložisek, tak, aby se mohl volně pootáčet. Pomocí páky a váhy se měří moment, kterým je elektromotor otáčen proti rotaci vrtule (pozor, neplést si s pojmem statický tah, který pro hodnocení vrtule je prakticky bezcenný). Výkon vrtule se dá vyjádřit velmi jednoduše
Výkon vrtule = moment x otáčky (6)
2.5 Statické versus letové poměry
Jak už bylo uvedeno, výchozí matematický model je založen na předpokladu relativní rychlosti mezi tekutinou a vrtulí a nezáleží na tom jestli se vrtule točí na stole nebo letí na letadle. To ovšem není v reálném světě pravda.
Statické měření je možno provést doma na stole. Je to jednoduché a pohodlné. Pokud se nechceme zabývat komplikovaným měřením proudu za letu nebo složitými výpočty, vlastně ani nic jiného nezbývá. Výsledky měření jsou zajímavé a důležité. Nechceme přece zničit motor už před startem.
Problém je ovšem s přenesením statického měření do letu. Mezi modeláři se traduje, že motor se za letu dost významně "odlehčí". Bohužel, tak snadné to není. Špatná zpráva je, že obecné závěry nelze dělat. Dobrá zpráva je, že si tuto skutečnost uvědomujeme a umíme s ní do jisté míry počítat.
Zhruba je možno říci následující:
Pokud použijeme vrtuli s malým úhlem natočení (poměr průměru a stoupání cca 2:1), motor se s velkou pravděpodobností za letu opravdu odlehčí. Může to být ale jen velmi málo a je lepší na to nespoléhat. Diagram zatížení v závislosti na rychlosti může mít dokonce "hrb" [4].
Pokud použijeme vrtuli s velkým úhlem natočení (zhruba "čtvercovou", poměr průměru a stoupání cca 1:1), veškeré odhady jsou z říše snů. Silně natočená vrtule je při statických testech pravděpodobně obtékána s výrazným odtržením proudu, za letu při návrhové rychlosti jsou poměry zcela jiné. Je dost pravděpodobné, že požadovaný výkon za letu dokonce naroste.
Statické měření není sice zdaleka dokonalé ale poskytuje jisté možnosti při porovnávání různých vrtulí, motorů, akumulátorů. Přinejmenším už není třeba střílet úplně naslepo ale je možno si pohony a jejich části snadno a rychle otestovat doma na stole, podle naměřeného proudu dimenzovat a teprve poté ověřit v provozu.
Poznámka:
V předchozím odstavci jsme pochopitelně předpokládali pouze měření a let na plný plyn.
Poznámka:
Statický tah vrtule závisí pouze na typu vrtule a na jejích otáčkách. Díky neznalosti této skutečnosti se zbytečně postavilo mnoho tahoměrů a zbytečně investovalo mnoho času při znovuobjevování dávno objeveného. Pro zjištění statického tahu stačí odměřit otáčky, zjistit si dva koeficienty a tah jednoduše vypočítat. Všechny běžné vrtule jsou dávno odměřené. Kdyby se vám nechtělo počítat (asi ne, proto ani vzoreček neuvádíme) stačí si otevřít např.
www.elektromodellflug.de (www spravuje německý elektro-guru G. Giesse), nainstalovat program DRIVE CALCULETOR a najít diagram pro danou vrtuli.
Jeden je pro ilustraci na obrázku. Stačí odměřit otáčky a odečíst statický tah (modrá křivka). Pomocí červené křivky lze pro dané otáčky odečíst výkon vrtule.
Program nabízí ovšem daleko větší možnosti.

3. VÝPOČTY
Pokud byste si rádi něco spočítali, je to docela snadno možné. Výchozí vzorec pro výkon (5) je možno pro danou vrtuli zjednodušit (Cp, ro, průměr považujeme za konstanty) na:
výkon = konstanta1 x otáčky ** konstanta 2 (7)
(konstanta2 = cca 3)
Obě konstanty je možno zjistit poměrně snadno sadou měření na dynamometru a jejich vyhodnocením. Nemusíte to ale dělat, konstanty pro velké množství běžných vrtulí již zpracovalo velké množství autorů. Tabulky jsou dostupné (a přeložené) např. na našich webových stránkách [6], [7]. Pro usnadnění výpočtu je možno (ale není nutno) použít Emeter a/nebo související programy které jsou volně dostupné.
Je ovšem nutno si uvědomit, že měření byla statická a výsledky pro letové poměry jsou pouze orientační.
Podobným způsobem, jen s jinými konstantami, je možno získat pro danou vrtuli i vztah mezi otáčkami a tahem. Pro dost přesné zjištění velikosti statického tahu stačí tedy naměřit otáčky a přepočíst tah. Konstanty pro některé vrtule jsou opět uvedené v programu pro Emeter (ale Emeter opět nepotřebujete).
4. MĚŘENÍ
Pomocí dostupné techniky (Eagletree Elogger, Emeter, přístroj CM50, výškoměr ALTI) byla provedena některá statická a letová měření. Měření trvají nějaký čas, při létání nesmí foukat atd, a není jich tedy mnoho. Nicméně poskytují alespoň částečný obrázek o vlastnostech pohonů, o kterých jsme dosud věděli hodně málo a tušili špatně.
K prvnímu měření
byl použit model Super Zoom od firmy Hacker, elektromotor AC MINI XT, baterie Lipol Dualsky Xpower 750-3s, regulátor Castle Creations Phoenix 25 v základním nastavení, vrtule GWS 9x5 HD.
Rychlost letu byla měřena za bezvětří na bázi 100 metrů, několikanásobným průletem.
Všechna data byla získána průměrováním několika měření. Nikdy nedošlo k výrazné odchylce. Proud byl měřen přístrojem CM50 v okamžicích podle povelů, přenášených RC systémem.

Statické měření:
10,2 V - 11,4 A - 8565 ot/min
Letové měření:
Vodorovný let na plný plyn: rychlost 56 km/hod, 8,8 A
Došlo tedy k poklesu proudu o 23%.
Poznámka: Zvolená baterie nebyla vhodná (malá kapacita), což se potvrdilo jejím krátkým životem.
Další měření bylo provedeno s elektrovětroněm Q10 o rozpětí cca 1800 mm a hmotnosti cca 500 gramů. Motor AC MINI T (převinutý na 6 závitů), baterie Xpower 1700-2s, sklopná vrtule Aeronaut 9x5.

Statické měření:
7,14V - 23,6 A - 8730 ot/min
Letové měření při stoupání v poměru cca 6 metrů/sec (tj. cca 180 metrů výšky za 30 sekund).
Provedeno 5 měření během 30 sekundového stoupání, průměrný odběr byl 20,5 A (pokles proudu byl velmi pozvolný). Motor je sice přetěžován ale v režimu časově krátkého zatížení bez regulace mu to zjevně nevadí. Pokles proudu byl pouhých 13 %, menší než jsme očekávali.
Závěry z našich měření:
1. Největší odběr proudu byl při statickém měření.
2. Pokles zatížení za letu nebyl ve srovnání se statickými zkouškami tak dramatický jak se očekávalo. Došlo k poklesu proudu o cca 10-20%.
3. Výsledků bylo dosaženo s vrtulemi o poměru průměru a stoupání zhruba 2:1.
Výsledky našich měření rozhodně nelze zobecňovat, zejména nemusí fungovat pokles proudu za letu. Mohou sloužit jen jako jisté vodítko k Vašim pokusům.
Poznámky k měření:
Statické měření je možno provádět v nejhorším případě s levným digitálním ampérmetrem. Lepší je pro tento účel analogový přístroj. Klešťové ampérmetry pro měření stejnosměrného proudu jsou dost drahé a pouze jednoúčelové. Rozhodně tedy stojí za úvahu použít přístroje, které jsou pro tato měření specializovány a často jsou víceúčelové. Dále existují přístroje, které měří v okamžiku podle povelu vysílače nebo přístroje, které shromažďují data během letu. Data se pak vyhodnocují na počítači a dají se libovolně zpracovat.
Přístroje, které naměří pouze maximální hodnoty během letu, jsou dobré jen pro velmi hrubou orientaci: naměří maximální proud - ale pravděpodobně při plném plynu těsně před startem, naměří maximální otáčky motoru - ale při jeho náhodném odlehčení. Pro vážnější práci se opravdu nehodí.
5. ZÁVĚR
Pokud jste čekali jednoznačný návod na řešení vrtule a souvisejícího pohonného řetězce a nedostali ho, nezlobte se. Ono to tak snadné není. Tím není jistě řečeno že optimální vrtule se nedá vypočíst. To je vyhrazeno několika specialistům a je zcela mimo možnosti běžného modeláře.
Optimalizace vrtule pro model F3D, letící konstantní "cestovní" rychlostí 350 km/hod, je ovšem úplně jiná úloha, než vybrat vhodnou vrtuli pro sportovní éro pro zábavu, které má létat v širokém rozsahu rychlostí. Předpokládáme, že naši čtenáři stojí spíše na té druhé straně. Specialisté pylonáři naši pomoc určitě nepotřebují.
Pokud jsme pomohli k alespoň částečnému vylepšení Vaší orientace v problematice, splnil článek účel a my děkujeme za trpělivost.
6. PODĚKOVÁNÍ
Děkuji RNDr Z. Hubáčkovi za významnou pomoc při psaní článku.
Ing. L. Bendovi děkuji za cenné kritické připomínky.
Literatura:
[1] Ash, Miley, Landman, Hyde: Evolution of Wright Flyer Propellers betweem 1903-1912 AIAA Journal 2001-0309
[2] Hořejší Milan: Profil, křídlo, vrtule
[3] Benda Lubomír: Vrtule - Seriál v časopise Modelář 1985
[4] Benda Lubomír: RCR 10/2005
[5] Hepperle Martin: Propulsion by propellers http://www.mh-aerotools.de
[6] Connolly: Prop talk http://www.hyperion.hk
[7] Hořejší Ivan: www.horejsi.cz
[8] Hubáček Zdeněk: Osobní sdělení
Článok prevzatý zo stránky : http://www.horejsi.cz/Pages/ListClanky.aspx
Nejnovější články v kategorii Letadla
Ochranné návleky na krídla a chvost.plochyhybrid
EPP Fokker DR1 Red Baron od VA-MODELS
Prosba YAK 54 8,5ccm CMP041 návod
Rozhodnutie Dopravneho úradu číslo 1/2019
| Autor | Zpráva |
|
podstanom modelár Příspěvků: 43 Moje modely Poslat zprávu |
super článok... mám lepší rozhľad... ale priznám sa, že neviem si vypočítať správnu vrtuľu na svoje éro. Je tu niekto čo by mi s tým pomohol??? heeeelp.... aké parametre treba vedieť k správnej vrtulke... potrebujem to na elektro-vetroňa |
|
niko modelár Příspěvků: 165 Moje modely Poslat zprávu |
Vrtule sú obrovské bludisko záhad. Ja len typujem podľa síly motora, otáčkach, nábehu atď. |
|
BOravec modelár Příspěvků: 576 Moje modely Poslat zprávu |
I keď tento článok tu visí nejaký ten piatok, voľba vrtule nie je otázkou nejakého tápania, ale cielená činnosť, ktorá sa nezaobíde bez aspoň základného výpočtu modelu. Je potrebné minimálne poznať rýchlosť, ktorou sa model má pohybovať vo vzduchu. a z toho určiť základné parametre t.j. stúpanie a priemer vrtule a potom skúšať ďalej. Inak program FLUENT vyžaduje trochu iný počítač, to si nikto na doma nekúpi. Samotný software je cenovo v kategórii pre bežného smrteľníka nedostupnej. Pre modelárske účely ale stačí software spomínaný v článku a jemu podobné, ktoré minimálne pomôžu tak, že zúžia oblasť rozmerov vrtulí, ktoré budeme skúšať. Úplne bez výpočtov sa to nedá. |
|
marianr modelár Příspěvků: 1467 Moje modely Poslat zprávu |
Keďže výrobcovia nezverejňujú charakteristiky vrtúľ (videl som len Aeronaut, v ich katalógu, zlé rozlíšenie), asi to až tak jednoduché nebude. |
|
BOravec modelár Příspěvků: 576 Moje modely Poslat zprávu |
Marian na stránke M.Seliga sú okrem polár profilov aj charakteristiky vrtúl - výhoda je, že oboje je namerané a nie vysnívané. Samozrejme nie sú tam všetky modelárske vrtule, ale i tak je výber dosť široký. Inak máš pravdu, jednoduchá problematika to nie je, navrhnúť vrtuľu je dosť náročné aj s použitím špičkových software. Na druhej strane už len rámcový prepočet zúži počet vrtúľ, ktoré budem na modeli testovať. Ešte dodám, myslím, že práve pán Hořejší v podobnej oblasti pracoval. |
- Přidat komentář



